传感器在使用过程中由于串入仪表或者采集系统，可能引入随机误差。其内部器件噪声和A/D量化噪声也会影响其高精度的输出性能。所以如何处理和削弱误差的影响，变得越来越重要，也得到了更广泛的重视。

传感器随机误差是由串入仪表的随机干扰、仪器内部器件噪声和A/D量化噪声引起的，室温和相对湿度等不稳定因素也是其产生的原因。在相同条件下测量同一量值时，单次测量无法发现规律，但在多次测量中，测量数据总体符合统计规律，测量值体现为实际量值的上下波动，随着测定次数的增加，误差的平均值将逐渐趋向于零。

数字滤波算法因为具有灵活性以及无需修改硬件就能达到不同的滤波效果等特点，使其得到了广泛的应用。它的主要优点如下：

（1）数字滤波只是一个计算过程，无需硬件，因此可靠性高，并且不存在阻抗匹配、特性波动、非一致性问题。模拟滤波器在频率很低时较难实现的问题，不会出现在数字滤波器的实现过程中。

（2）只要适当改变数字滤波程序有关参数，就能方便的改变滤波特性，因此数字滤波使用时方便灵活。

常用的数字滤波算法主要有：克服大脉冲干扰的数字滤波算法、抑制小幅度高频噪声的平均滤波法和复合滤波法。

一、克服大脉冲干扰的数字滤波算法

克服由仪器外部环境偶然因素引起的突变性扰动或一起内部不稳定引起的误码等造成的尖脉冲干扰。通常采用简单的非线性滤波法。

1.限幅滤波法（又称程序判别法）

通过程序判断被测信号的变化幅度，从而消除缓变信号中的尖脉冲干扰。具体方法是，依赖已有的时域采样结果，将本次的采样值与上次的采样值进行比较，若它们的差值超出允许范围，则认为本次采样值受到了干扰，应予易除。

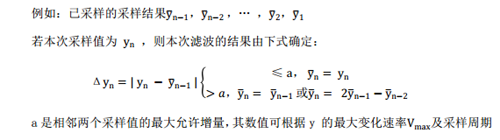
2.中值滤波法

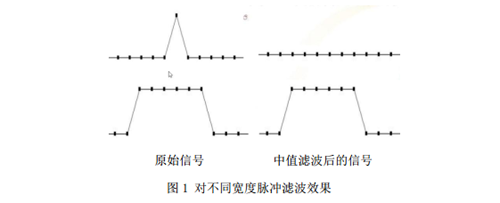
中值滤波是一种典型的非线性滤波器，它运算简单，在滤波脉冲噪声的同时可以很好地保护信号的细节信息。对某一被测参数连续采样N次（一般N应为奇数），然后将这些采样值进行排序，选取中间值作为本次采样值。对温度、液位等缓慢变化的被测参数，采用中值滤波法一般能收到良好的滤波效果。

二、抑制小幅度高频噪声的平均滤波法

小幅度高频电子噪声：电子器件热噪声、A/D量化噪声等。

通常采用具有低通特性的线性滤波器：算术平均滤波法、滑动平均滤波法、加权滑动平均滤波法等。

1.算术平均滤波法

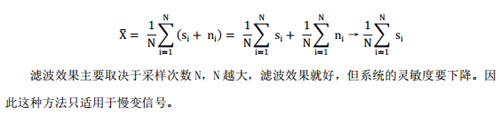
2.滑动平均滤波法

对于采样速度较慢或要求数据更新率较高的实时系统，算术平均滤波法无法使用的。

滑动平均滤波法把N个测量数据看成一个队列，队列的长度固定为N，每进行一次新的采样，把测量结果放入队尾，而去掉原来队首的一个数据，这样在队列中始终有N个“最新”的数据。

平滑度高，灵敏度低；但对偶然出现的脉冲性干扰的抑制作用差。实际应用时，通过观察不同N值下滑动平均的输出响应来选取N值以便少占用计算机时间，又能达到最好的滤波效果。

3.加权滑动平均滤波法

增加新的采样数据在滑动平均中的比重，以提高系统对当前采样值的灵敏度，即对不同时刻的数据加以不同的权。通常越接近现时刻的数据，权取得越大。

三、复合滤波法

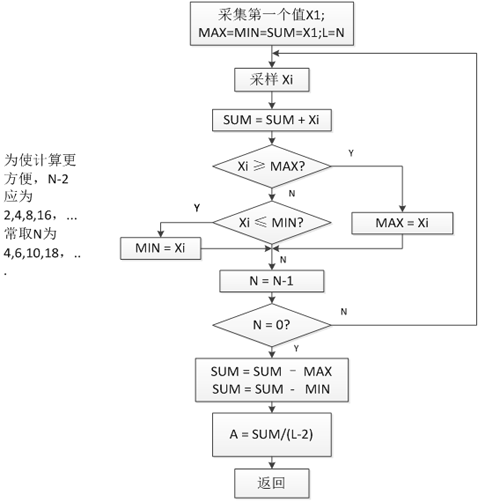
在实际应用中，有时即要消除大幅度的脉冲干扰，又要做数据平滑。因此常把前面介绍的两种以上的方法结合起来使用，形成复合滤波。我们将用去极值平均滤波算法进行示例。

去极值平均滤波算法：先用中值滤波算法滤除采样值中的脉冲性干扰，然后把剩余的各种采样值进行平均滤波。连续采样N次，剔除其最大值和最小值，再求余下N-2个采样的平均值。显然，这种方法既能抑制随机干扰，又能滤除明显的脉冲干扰。